备课是上好课的前提。集体备课就是教师根据课程标准的要求和教材特点，结合学生的实际情况，选择最科学的教法和学法，为优质高效的课堂教学做好充分准备。为了充分发挥集体智慧，促进以老带新、以新促老、集思广益、博采众长，真正实现资源共享，为了结合我校十三五课题《基于数学思考构建小学数学智慧课堂的实践研究》。5月7日下午，数学教研组在三楼东办公室进行了“体验知识转化策略 提高解决问题能力”为主题的集体备课活动。首先，高敏老师介绍的《解决问题的策略-转化》一课的整体设计，组内教师进行研讨交流。

主备教师

高敏

集体讨论时间

2019.5.7

课题

解决问题的策略-转化

所属单元

第七单元

教学

目标

1. 让学生初步学会转化的策略分析问题，灵活确定解决问题的思路，并能根据问题的特点确定具体的转化方法，从而有效的解决问题。

2. 让学生通过回顾曾经运用转化策略解决问题的过程，从策略的角度进一步体会知识间的联系，感受转化的应用价值。

3. 让学生进一步积累运用转化的策略解决问题的经验，增强解决问题的策略意识，主动克服解决问题过程中遇到的困难，获得成功的体验。

重难点

重点：学生探索怎样将不规则图形转化成规则图形。

难点：引导学生通过合作、讨论、交流，运用转化的策略解决问题。

教  学  过  程

参备意见

教学设计

一、初步交流，确定策略

师：我们以前已经解决过很多数学问题。今天这一节课，我们要进一步解决新的数学问题，看看能解决什么新的问题。

1．出示例1的两个图形。

师：请同学们仔细观察这两个图形，这是两个完全不一样的平面图形，

学生读问题，开动脑筋，独立思考怎样比较这两个图形的面积。

2．引导思考：我们观察这两个图形，是两个比较复杂的、不规则的图形，不能直接比较大小。大家通过观察，找到比较方法了没？

说明：同学们发现、交流的方法都可以比出大小，并且想到能够把不规则的图形变成规则的图形，怎么变呢？请在练习纸上想想画画，看看可以怎样做。

3.小组交流想法。

师：能不能变成规则图案，把你的方法介绍给大家。指名演示

学生可能有两种想法：

(1)用数方格的方法计算每个图形的面积后再比较。

(2)联系自己的知识经验，将两个图形分别转化成规则图形，再比较它们的面积。

引入：看来运用转化的方法也能帮助我们解决生活中的实际问题，这节课我们就来学习用转化的策略解决问题。

（板书课题；解决问题的策略——转化）

二、探究新知

教学例1。

师：怎样把这两个图形分别转化成长方形呢？自己在方格纸上画一画。

学生交流。

教师提问：刚才我们在解决这个问题时，为什么要把原来的图形转化成长方形？

学生回答：原来的图形比较复杂，不容易看出每个图形的面积，不便于直接比较面积的大小。转化成长方形后容易看出每个图形的面积，也就便于比较了。

师：在以前的学习中我们曾经运用转化的策略解决过哪些问题？

学生发言，教师有选择地板书。

师：这些运用转化策略解决问题的过程有什么共同点？

学生讨论交流。

教师明确：都是把新的问题转化成熟悉的或已经会解决的问题。

（板书：未知--已知）

教师小结：转化是一种常见的、极其重要的解决问题的策略。在我们以往的学习中经常用到这一策略分析并解决问题。以后再遇到一个陌生问题时，你会怎样想？

三、巩固运用

教师相机引导完成“练一练”及练习中有关运用转化策略的问题。

空间与图形的领域

1.练习十六第1题  

出示方格纸上的两个图形，让学生思考怎样计算右边图形的周长比较简便。这里什么变了什么不能变？

引导学生明确：可以把这个图形转化成长方形计算周长。

提问：如果每个小方格的边长是1厘米，右边图形的周长是多少厘米？

2、练习十六第2题   用分数表示图中的涂色部分

先独立看图填空，再交流是怎样想到转化的方法的，以及分别是怎样转化的？什么变了什么没变？

3、练一练

指导完成“练一练”平移方法。

4、练习十六第3题

先独立解答，再交流和评点。  

四、课堂小结

师：今天学习了什么内容？你对转化的策略有了哪些新的认识？

学生自由发言。

林耀霞：导入部分比较简单，可以尝试用故事导入

陈雨老师建议第一个小组活动，在比较两个不规则图形的大小时，学生说出的方法有：转化和数格子。其实是一个很好的教学契机，也正是学生的原有知识经验的体现。而老师直接将学生关于数格子的思考回避了，将原来的认知冲突规避了，学生直入主题——切割、补齐成一个规则的数学图形， 也就降低学生思考的难度，把原来学生的想法回避掉了。这时，教师如果能充分发挥学生的主体地位，组织学生进行了一系列的操作体验活动如看一看、数一数、剪一剪、拼一拼，借助集体的智慧找到解决问题的方法，主要有：1、数方格。2、剪剪拼拼。3、平移、旋转。接着引导学生进行比较：你们比较喜欢哪种方法？为什么？使学生感悟到：在这一类题目的处理中，关键是把不规则的图形转化成规则图形，数格子和剪拼虽然能解决问题，但耗时操作麻烦，同时也优化了方法。

主备教师

高敏

集体讨论时间

2019.5.7

课题

解决问题的策略-转化

所属单元

第七单元

教学

目标

1.让学生初步学会转化的策略分析问题，灵活确定解决问题的思路，并能根据问题的特点确定具体的转化方法，从而有效的解决问题。

2.让学生通过回顾曾经运用转化策略解决问题的过程，从策略的角度进一步体会知识间的联系，感受转化的应用价值。

3.让学生进一步积累运用转化的策略解决问题的经验，增强解决问题的策略意识，主动克服解决问题过程中遇到的困难，获得成功的体验。

重难点

重点：学生探索怎样将不规则图形转化成规则图形。

难点：引导学生通过合作、讨论、交流，运用转化的策略解决问题。

教  学  过  程

参备意见

教学设计

一、故事引入，初步体验转化。

阿普顿是美国普林斯顿大学数学系毕业的高材生，对没有大学文凭的爱迪生有点瞧不起。有一次，爱迪生让他测算一只梨形灯泡的容积。于是，他拿起灯泡，测出了他的直径高度，然后加以计算。但是灯泡不具有规则形状：它像球形，又不像球形；像圆柱体，又不像圆柱体。计算很复杂。即使是近似处理也很繁琐。他画了草图，在好几张白纸上写满了密密麻麻的数据算式，也没有算出来。

爱迪生等了很长时间，也不见阿普顿报告结果。他走过来一看，便忍不住笑出了声，“你还是换种方法吧！”只见爱迪生取来一杯水。轻轻地往阿普顿刚才反复测算的灯泡里倒满了水，然后把水倒进量筒，几秒种就测出了水的体积，当然也就算出了灯泡的容积。这时羞红了脸的阿普顿傻呆呆地站在一旁，恨不得找条地缝钻下去。

这个故事让你联想到什么？将求不规则物体的体积转化成求水的体积，用到了一个重要的策略——转化。

二、探究新知

出示例1的两个图形。

师：请同学们仔细观察这两个图形，这是两个完全不一样的平面图形，

学生读问题，开动脑筋，独立思考怎样比较这两个图形的面积。

3．引导思考：我们观察这两个图形，是两个比较复杂的、不规则的图形，不能直接比较大小。大家通过观察，找到比较方法了没？

说明：同学们发现、交流的方法都可以比出大小，并且想到能够把不规则的图形变成规则的图形，怎么变呢？请在练习纸上想想画画，看看可以怎样做。

3.小组交流想法。

师：能不能变成规则图案，把你的方法介绍给大家。指名演示

学生可能有两种想法：

(1)用数方格的方法计算每个图形的面积后再比较。

(2)联系自己的知识经验，将两个图形分别转化成规则图形，再比较它们的面积。

引入：看来运用转化的方法也能帮助我们解决生活中的实际问题，这节课我们就来学习用转化的策略解决问题。

（板书课题；解决问题的策略——转化）

二、探究新知

教学例1。

师：怎样把这两个图形分别转化成长方形呢？自己在方格纸上画一画。

学生交流。

教师提问：刚才我们在解决这个问题时，为什么要把原来的图形转化成长方形？

学生回答：原来的图形比较复杂，不容易看出每个图形的面积，不便于直接比较面积的大小。转化成长方形后容易看出每个图形的面积，也就便于比较了。

师：在以前的学习中我们曾经运用转化的策略解决过哪些问题？

学生发言，教师有选择地板书。

师：这些运用转化策略解决问题的过程有什么共同点？

学生讨论交流。

教师明确：都是把新的问题转化成熟悉的或已经会解决的问题。

（板书：未知--已知）

教师小结：转化是一种常见的、极其重要的解决问题的策略。在我们以往的学习中经常用到这一策略分析并解决问题。以后再遇到一个陌生问题时，你会怎样想？

巩固运用

教师相机引导完成“练一练”及练习中有关运用转化策略的问题。

空间与图形的领域

1.练习十六第1题  

出示方格纸上的两个图形，让学生思考怎样计算右边图形的周长比较简便。这里什么变了什么不能变？

引导学生明确：可以把这个图形转化成长方形计算周长。

提问：如果每个小方格的边长是1厘米，右边图形的周长是多少厘米？

2、练习十六第2题   用分数表示图中的涂色部分

先独立看图填空，再交流是怎样想到转化的方法的，以及分别是怎样转化的？什么变了什么没变？

3、练一练

指导完成“练一练”平移方法。

4、练习十六第3题

先独立解答，再交流和评点。  

四、课堂小结

师：今天学习了什么内容？你对转化的策略有了哪些新的认识？

学生自由发言。

周爽：新授部分不够详细，回顾转化实例，感受转化的价值是个重要环节，要充分让学生感受体会。

贾鹤：教师在设计教案时要在对教材进行深度研读的基础上，真正能从学生的已有知识经验和生活经验出发，找准学生的最近发展区，激发学生的认知冲突。策略重在体验，正是学生有了困惑、有了理解的难度、有了认知的冲突，对转化的策略才可能有较深的认识，只有学生有了这样的体验，才会有顿悟后的“解惑”。

陈银：这个环节，为了让学生在思想上从策略的高度主动运用转化的策略，高老师设计了图形转化、数形转化、实际问题转化等层次的练习。由于学生已经对转化的策略有了较深的认识和理解，因此在练习中，高老师也基本是放手让学生自主思考，自主练习。通过计算、图形、阴影、比赛等一系列有层次的练习，让学生在运用转化策略的同时，感受到了转化策略的美妙。

主备教师

高敏

集体讨论时间

2019.5.7

课题

解决问题的策略-转化

所属单元

第七单元

教学

目标

1.让学生初步学会转化的策略分析问题，灵活确定解决问题的思路，并能根据问题的特点确定具体的转化方法，从而有效的解决问题。

2.让学生通过回顾曾经运用转化策略解决问题的过程，从策略的角度进一步体会知识间的联系，感受转化的应用价值。

3.让学生进一步积累运用转化的策略解决问题的经验，增强解决问题的策略意识，主动克服解决问题过程中遇到的困难，获得成功的体验。

重难点

重点：学生探索怎样将不规则图形转化成规则图形。

难点：引导学生通过合作、讨论、交流，运用转化的策略解决问题。

教  学  过  程

参备意见

教学设计

一、故事引入，初步体验转化。

阿普顿是美国普林斯顿大学数学系毕业的高材生，对没有大学文凭的爱迪生有点瞧不起。有一次，爱迪生让他测算一只梨形灯泡的容积。于是，他拿起灯泡，测出了他的直径高度，然后加以计算。但是灯泡不具有规则形状：它像球形，又不像球形；像圆柱体，又不像圆柱体。计算很复杂。即使是近似处理也很繁琐。他画了草图，在好几张白纸上写满了密密麻麻的数据算式，也没有算出来。

爱迪生等了很长时间，也不见阿普顿报告结果。他走过来一看，便忍不住笑出了声，“你还是换种方法吧！”只见爱迪生取来一杯水。轻轻地往阿普顿刚才反复测算的灯泡里倒满了水，然后把水倒进量筒，几秒种就测出了水的体积，当然也就算出了灯泡的容积。这时羞红了脸的阿普顿傻呆呆地站在一旁，恨不得找条地缝钻下去。

这个故事让你联想到什么？将求不规则物体的体积转化成求水的体积，用到了一个重要的策略——转化。

二、观察交流，明确转化的策略

1、出示例1：

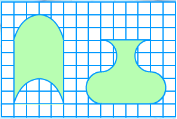
师：这两个图形像什么啊？你觉得这两个图形的面积相等吗？仔细观察图形，你准备怎样比较这两个图形的面积。

师：思考后再在小组里交流自己是怎样想的。

学生可能有两种想法：（1）数方格计算每个图形的面积后再比较。提醒学生把方格线补画完整。（2）将两个图形分别转化成长方形，再比较它们的面积。

如果学生说出这一种想法，则引导用数方格的方法要注意什么？

如果没有学生说出第二种想法，则引用书上：能否把原来的图形都转化成长方形，再比一比。

自己在方格纸上画一画。结合学生回答实物投影演示学生方法。

交流：（1）第一个图形是怎样转化成长方形的？你是怎样想到把上面的半圆进行平移的？上面的半圆向什么方向平移了几格？（2）第二个图形是怎样转化成长方形的？你是怎样想到把左右两个半圆进行旋转的？左右两个半圆分别旋转了多少度？（3）现在你怎样看出这两个图形的面积相等吗？比较面积是否相等什么可以变什么不能变？

小结：刚才我们在解决这个问题时，为什么要把原来的图形转化成长方形？（原来的复杂，转化后简单便于比较）  板书：不规则 规则

三、回顾转化实例，感受转化的价值

引导：实际在以往的学习中，我们曾经多次运用转化的策略解决过哪些问题？小组在一起讨论。

学生充分列举，教师根据学生回答出示教材图示。

曾经在推导很多图形的面积或体积公式时用过转化策略

学生小组交流后汇报时引导学生说清楚什么变了什么不能变，结合课件演示。
 （1）推导三角形面积公式时，把两个完全一样的三角形拼成一个平行四边形，就把求三角形面积的问题转化成求平行四边形的面积。
 （2）一个三角形通过切割、旋转也能把它转化成一个平行四边形（也就是等积变形），从而求出它的面积。
 （3）推导梯形面积公式时……
 （4）推导圆形面积公式时，通过切拼把圆转化成长方形来求面积。
 （5）推导圆柱体积公式时，也把圆柱通过切拼转化成长方体求体积。
 （6）推导圆锥体积公式时，又把圆锥转化成圆柱来求体积。
师：这些运用转化的策略解决问题的过程有什么共同点？（把新问题转化成熟悉的或者已经解决过的问题。）板书：新知旧知

小结：转化是一种常见的、极其重要的解决问题的策略。在我们以往的学习中，早就运用这一策略分析并解决问题了。以后再遇到一个陌生问题时，你会怎样想？

师：不仅在求面积、体积而且在求周长的问题上，我们也曾经运用转化策略。引导学生回忆圆周长的测量方法。（三角形内角和等）

通过刚才同学们举的许多例子证明转化的思路对我们学习空间与图形帮助很大，实际在我们学习的计算中也多次用到了转化的思路，想想看在哪用到过的？（小数乘法与分数除法等等）

四、巩固运用    

1．完成练习十六第1题。

(1)出示方格纸上的图形，让学生思考怎样计算右边图形的周长比较简便。

引导学生明确：可以把这个图形转化成长方形计算周长。

(2)提问：如果每个小方格的边长是1厘米，右边图形的周长是多少厘米？

进一步提问：解决这个问题的策略是什么？

4．完成练习十六第9题。

先独立看图填空，再交流是怎样想到转化方法的，分别是怎样转化的。

3．完成练习十六第6题。

(l)出示问题，指导学生理解图意。

明确图中每一排的点分别表示每一轮参加比赛的球队，把两个点合成一个点的过程表示进行了一场比赛。单场淘汰制就是每场比赛都淘汰1支球队。

(2)引导学生数一数，一共要进行多少场比赛后才能产生冠军？

(3)师：如果不画图，有更简便的计算方法吗？如果有16支球队，产生冠军一共要比赛多少场？

2．完成练习十六第3题。

先独立解答，再交流、评点。

四、课堂小结

师：今天学习了什么内容？你对转化的策略有了哪些新的认识？

学生自由发言。